Rotation de particules asymétriques avec de la lumière ordinaire
La possibilité de faire tourner des systèmes optiquement offre de nouvelles perspectives pour le contrôle de micro-objets, avec des applications dans divers domaines, notamment pour les microsystèmes électromécaniques (ou MEMS en anglais), pour la biomanipulation ou l’optofluidique [1-3]. Certaines configurations profitent de la forme spéciale d’objets 3-D, de la pression de radiation et de la diffusion de la lumière ordinaire, alors que d’autres utilisent le moment angulaire de la lumière, qu’il soit de spin (polarisation circulaire) ou orbital.
Basé sur un mécanisme complètement différent, nous avons montré que l’on pouvait mettre en rotation des objets 2-D asymétriques (voir l’insert de la figure) en utilisant des ondes planes issues soit d’un laser ordinaire ou du rayonnement d’un corps noir [4]. Ces objets sont des cames avec un nombre de pales variant de 1 à 8 imprimées sur des transparents pour imprimante. La lumière diffusée par ces objets transporte du moment angulaire orbital [5]. Par conservation du moment angulaire orbital, les objets diffractants doivent acquérir eux même du moment angulaire orbital. La conservation de l’énergie est assurée par un faible décalage en fréquence de la lumière diffractée. Les objets flottent à la surface de l’eau. Nous observons une rotation à vitesse constante dont la fréquence dépend de l’intensité lumineuse et du degré d’asymétrie de l’objet (voir figure). La rotation a lieu pour des puissances lumineuses de l’ordre de 100 mW, que ce soit avec la source laser ou la source de lumière blanche issue du corps noir. Nous avons exclu la possibilité de transfert du moment angulaire par absorption ou par effet thermo-capillaire. La seule origine possible du couple de rotation est la diffraction par les bords de l’objet et la conservation du moment angulaire.
De telles rotations peuvent trouver des applications en optofluidique, pour mettre en mouvement par la lumière des micromoteurs. Ces derniers engendreraient l’entraînement de flux de liquide. Cela pourrait aussi apporter un éclairage nouveau sur le problème de l’homochiralité de la vie. En effet, si l’on considère le problème inverse, simplement avec le soleil et des particules en rotation à la surface de l’eau, pourrait-on imaginer que le couplage de la lumière et de la rotation puisse induire de l’asymétrie sur des objets initialement symétriques et ainsi induire de la chiralité.
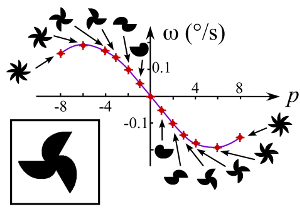
Figure : Vitesse de rotation ω des cames en fonction du nombre de pales p. Les croix correspondent aux valeurs expérimentales. Le trait plein est un guide pour les yeux. Insert : image d’une came à 3 pales.
Références
1. D.G. Grier, Nature 424, 810 (2003).
2. A.M. Yao and M. Padgett, Adv. Opt. Photon. 32, 161 (2011).
3. K. Kim, J. Guo, Z. X. Liang, F.Q. Zhu and D.L. Fan, Nanoscale 8, 10471 (2016).
4. O. Emile and J. Emile, Opt. lett. 41, 211 (2016).
5. O. Emile, M. le Meur and J. Emile, Phys. Rev. A 89, 013846 (2014).






